This is a continuation of Probability: Introduction to Measure Theory — Part of my probability theory. Today we’ll focus on how probability is defined through measure theory and how we can derive all the axioms of probability through the axioms of measure theory.

The universe

For any measure, we need to define the universal set and the sigma algebra. In the last article, we used atoms as the building blocks of the real world. The universal set Ψ was the set of all atoms in the universe. Analogous to atoms, the building blocks of a probability universe are outcomes — a single possible result of an experiment. So the universal set here is the set of all outcomes — the sample space. Denote by Ω, this set is our replacement for Ψ.

The Sigma Algebra

Now we know our universe. The sigma algebra is a set of the subsets of the universe. Each subset of the sample space is a set of outcomes. This is also known as an event. So our sigma algebra is the set of all events. Let’s denote that by F.

So (Ω, F) together form the measurable space.

Let’s make sure F satisfies the axioms of a sigma-algebra.

Axiom 1: Null space

The null space in this context refers to an impossible event. This clearly exists in our sigma algebra as the set with no outcomes.

Axiom 2: Complement

For every outcome in the experiment, we would know when the outcome doesn’t occur. For example, in a coin toss, if a tail occurs then the head doesn’t occur and if the head occurs then the tail doesn’t. So for every event, we also have it’s complement in the sigma algebra.

Axiom 3: Union of sets

Each event is formed from it’s constituent outcomes. So if we have two or more events, we can just combine their outcomes to create a newer event. This follows the axiom that union of elements of the sigma algebra is another element of the sigma algebra

All of the axioms apply for this sigma algebra. This means we do have a measurable space.

The Probability Measure

A measure is a function from the sigma algebra to the real numbers. The probability measure is slightly special. it is defined as:

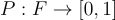
Instead of its range being the entirety of real numbers, it’s range is from 0 to 1 (inclusive). But, we still need it to be a measure. So we will need to provide some more constraints to this function so that it acts as a valid measure in our measure space. The constraints are simply the axioms of a measure:

Axiom 1: The measure must be non-negative

The range of our measure is from 0 to 1, so obviously it is non-negative. So we don’t need to change anything here.

Axiom 2: null set maps to 0

The null set in our measurable space was the event that is impossible to occur. This means that one of the constraints of our probability measure must be that the probability of an empty set is 0.

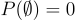
Axiom 3:

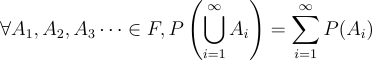
Since we can’t be sure of this property unless we know the actual definition of the probability function, we’ll just have to pass on this axiom as one of the axioms probability. Given a particular distribution (Gaussian, Uniform, etc), we can test this probability to ensure that they are valid measures.

Additional Axiom for probability

Probability has an additional axiom apart from the above 3:

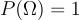
So the probability of the sample space is 1. Essentially this means that something in the sample space must occur for a given experiment

How these translate to the axioms of probability

Now we have a probability measure that satisfies the axioms of a measure and has an additional probability. It’s not any work at all to show how these are directly related to the original Kolmogorov’s axioms for probability:

Axiom of probability 1:

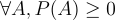
Axiom of probability 2:

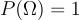
Axiom of probability 3:

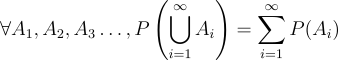
Measure theory simply bases these axioms on even more foundational axioms.

So there we have it: We’ve rigorously defined what the probability measure. This still does not explain to us what probability actually is. But it does give us a mathematical support to know how probability works and we should go about using it.

We actually don’t need all the constraints

In reality, the two constraints:

• The range of probability is [0, 1]
• P(Ω) = 1

We can actually get one of these using the others (homework).

Conclusion

In this article, we used measure theory explained in the previous article to derive a probability measure. Next, we’ll talk about certain properties and modifications to the probability measure including conditional probability and Bayes’ theorem.